数据结构
约 1830 字大约 6 分钟
2025-03-05
1.绪论
1.1 数据结构的基本概念
- 数据:数据是信息的载体,符号的集合、所有能输入到计算机中并能被计算机程序处理的符号的集合,数据是计算机程序加工的原料
- 数据元素:数据的基本单位,通常作为一个整体进行考虑和处理。一个数据元素可由若干数据项组成
- 数据项:构成数据元素的不可分割的最小单位
- 数据对象:数据对象是具有相同性值的数据元素的集合,是数据的一个子集
- 数据结构:数据结构是相互之间存在一种或多种特定关系的数据元素的集合。
1.2 数据结构的三要素
- 逻辑结构(数据元素之间的逻辑关系):
- 线性:线性表、栈、队列
- 非线性:树、图、集合
- 物理结构(数据结构在计算机中的表示):顺序存储、链式存储、索引存储、散列存储
- 数据运算
1.3 算法基本概念
定义:算法是对特定问题求解步骤的一种描述,它是指令的有限序列,其中的每条指令表示一个或多个操作
算法的特性:
- 有穷性:一个算法必须总在执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每条指令必须有确定的含义,对于相同的输入只能得到相同的输出。
- 可行性:算法中描述的操作都可以通过已经实现的基本运算执行有限次来实现。
- 输入:一个算法有零个或多个输入,这些输入取自于某个特定的对象的集合。
- 输出:一个算法有一个多个输出,这些输出是与输入有着某种特定关系的量。
1.4 算法的时间复杂度
计算步骤:
- 找到一个最深层循环
- 分析该循环的执行次数 x 与 问题规模 n 的关系:x=f(n)
- x 的数量级 O(x) 就是该算法的时间复杂度
时间复杂度对比:常对幂指阶
O(1) < O(log2n) < O(n) < O(nlog2n) < O(n2) < O(n3)< O(2n) < O(n!) < O(nn)
2.线性表
2.1 线性表
定义:线性表是具有相同数据类型的n(n>0)个数据元素的有限序列。(其中n为表长,当n=0时线性表是一个空表)
存储结构:
- 顺序存储结构:顺序表(适合查找)
- 链式存储结构:链表(适合增删、扩容)
2.2 顺序表
定义:顺序表是用顺序存储的方式实现线性表顺序存储。把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中,元素之间的关系由存储单元的邻接关系来体现。
特点:
- 随机访问,查询时间复杂度O(1)
- 拓展容量不方便
- 存储密度高,每个节点只存储数据元素
- 插入删除操作不方便,需要移动大量元素,O(n)
2.3 链表
链表可以分为单链表、双链表、循环链表
| 单链表 | 双链表 | 循环链表 | |
|---|---|---|---|
| 定义 | 用链式存储实现了线性结构,一个结点存储一个数据元素,各结点间的前后关系用一个指针表示 | 各结点间的前后关系用两个个指针表示 | 最后一个结点的指针不是NULL,而是指向头结点 |
| 优点 | 不要求大片连续空间,改变容量方便 | 可以找到前驱和后继,可进可退 | 从表中任一节点出发均可找到表中其他结点 |
| 缺点 | 不可随机存取,要耗费一定空间存放指针 | 增加删除节点复杂,需要多分配一个指针存储空间 | 维护成本大 |
3.栈和队列
3.1 栈
定义:栈是一种特殊的线性表,只允许在一端(栈顶top)进行插入或删除操作
特点:元素后进先出
应用场景:
- 撤销操作
- 浏览器历史记录
- 递归算法
3.2 队列
定义:队列也是一种特殊的线性表,在表的一端(队尾)插入,表的另一端(队头)进行删除操作
特点:元素先进先出
应用场景:
- 广度优先搜索算法
- 消息队列系统
4.树
4.1 基本概念
定义:树是一个有n个节点的有限集合,是一种递归的数据逻辑结构。当n=0时为空树,且非空树满足:有且仅有一个特定的称为根的节点
非空树特点:
- 有且仅有一个根节点
- 没有后继的结点称为“叶子结点”
- 有后继的结点称为“分支结点”
- 除了根节点外,任何一个结点都有且仅有一个前驱
- 每个结点可以有0个或多个后继
树的属性:
- 结点的层次(深度)——从上往下数
- 结点的高度——从下往上数
- 结点的度--有几个孩子(分支)
- 树的度一-各结点的度的最大值
常见属性关系和计算公式:
- 树中的结点数=总度数+1(1为根节点)
- 度为m的树、m叉树的区别:
- 树的度--各结点的度的最大值
- m叉树--每个结点最多只能有m个孩子的树
- 度为 m 的树第 i 层最多有
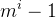 个结点
个结点 - 高度为 h 的 m 叉树至多有个结点
- 高度为h的m叉树至少有h个结点;高度为h、度为m的树至少有h+m-1个结点。 常见考点6: 具有n个结点的m叉树的最小高度为
4.2 二叉树
定义:由一个根节点、左子树、右子树组成,其中左子树和右子树又分别是一棵二叉树
特点:
- 每个结点至多只有两棵子树
- 左右子树不能颠倒(二叉树是有序树)
特殊二叉树:
- 满二叉树:高度为 h ,含有 2^h -1 个结点的 二叉树
- 完全二叉树:在满二叉树的基础上,可以去掉若干个编号更大的结点
- 二叉排序树:左子树关键字 < 根节点关键字 < 右子树关键字
- 平衡二叉树:左右子树深度不超过1
4.3 二叉树遍历
4.3.1 前中后序遍历
技巧:
- 前序遍历:根左右
- 中序遍历:左根右
- 后序遍历:左右根
例题:
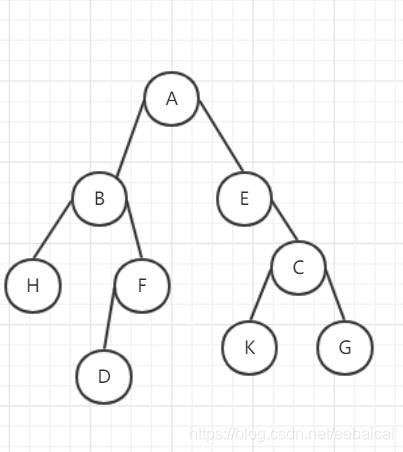
例:已知二叉树前序遍历是 ABHFDECKG ,中序遍历序列是 HBDFAEKCG ,它的后序遍历序列是()
- 因为前序遍历是 ABHFDECKG ,所以根节点为 A;再根据中序遍历,有 HBDF 为左子树,EKCG 为右子树
- 递归,根据前序遍历,知 B是根节点;根据中序遍历,有 H是左子树、DF为右子树
- 逐步推理....得后序遍历为 HDFBKGCEA
4.3.2 层序遍历
定义:一层一层,从上往下的遍历
实现:队列
5.图
待补充